T-SNE

T-SNE : L’algorithme de réduction de dimensionnalité appelé t-distributed stochastic neighbor embedding (t-SNE) est un algorithme d’apprentissage non supervisé. Développé par Laurens van der Maaten et Geoffrey Hinton, il permet d’analyser des données décrites dans des espaces à forte dimensionnalité (via un grand nombre de descripteurs) pour les représenter dans des espaces à deux ou trois dimensions. Cet algorithme est très utilisé car il facilite la visualisation de données ayant beaucoup de descripteurs.

T-SNE est un algorithme non-linéaire de “feature extraction” qui construit une nouvelle représentation des données de telle sorte que les données proches dans l’espace original aient une probabilité élevée d’avoir des représentations proches dans le nouvel espace. A l’inverse, les données qui sont éloignées dans l’espace original, ont une probabilité faible d’avoir des représentations proches dans le nouvel espace. En pratique la similarité entre chaque paire de données, dans les deux espaces, est mesurée par le biais de calculs probabilistes basés sur des hypothèses de distribution. Et les nouvelles représentations se construisent de telle sorte à minimiser¹ la différence² entre les distributions de probabilités mesurées dans l’espace original et celles du nouvel espace.

Cependant, même si cet algorithme crée une distribution qui respecte la proximité entre les objets les plus proches, la nouvelle représentation ne respecte pas forcément les  distances et les densités de distribution des données originales.

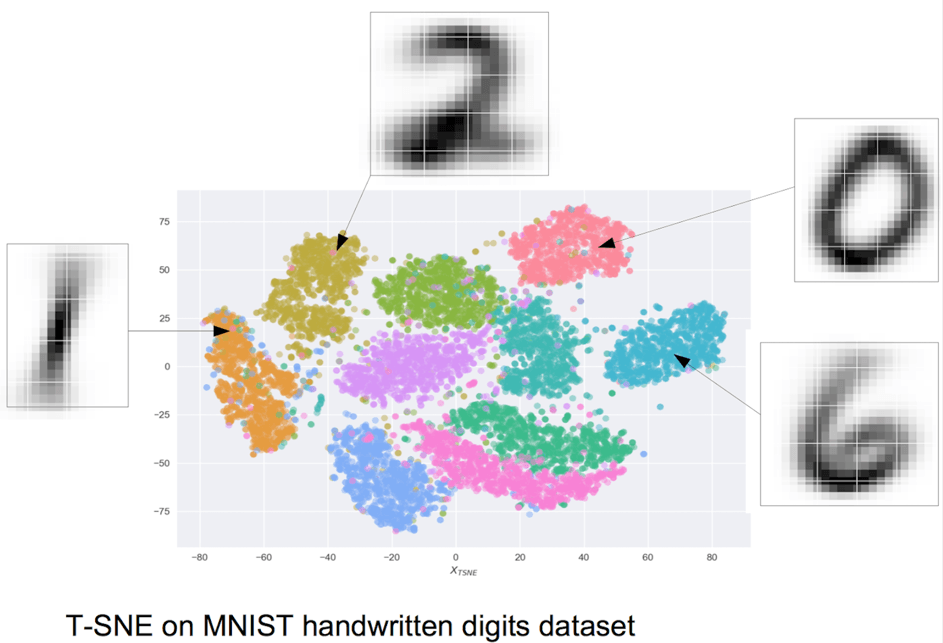
Dans l’exemple suivant, on a appliqué l’algorithme T-SNE, au célebre jeu de données MNIST, des chiffres écrits à la main (0, 1 et 2 dans cet exemple). Chaque chiffre est une image de 28×28 pixels. Chaque pixel étant un descripteur, les données existent dans un espace à 28×28=784 dimensions.  Ces données ont été traitées par l’algorithme t-SNE, afin de les projeter dans un espace à 2 dimensions (les deux axes de l’image). L’image au centre correspond à la projection de chaque image dans ce nouvel espace, chaque chiffre étant associé à une couleur différente (ici, la couleur orange représente le chiffre “1”, la couleur rouge le chiffre “0”). Comme on le constate, la représentation fournie par l’algorithme t-SNE permet de séparer et de former des groupes bien distincts pour chacun des chiffres du jeu de données.

1. En utilisant l’algorithme de descente de gradient stochastique.
2. Mesurée en considérant la divergence de Kullback-Leibler.