K-means (ou K-moyennes) : C’est l’un des algorithmes de clustering les plus répandus. Il permet d’analyser un jeu de données caractérisées par un ensemble de descripteurs, afin de regrouper les données “similaires” en groupes (ou clusters).
La similarité entre deux données peut être inférée grâce à la “distance” séparant leurs descripteurs ; ainsi deux données très similaires sont deux données dont les descripteurs sont très proches. Cette définition permet de formuler le problème de partitionnement des données comme la recherche de K “données prototypes”, autour desquelles peuvent être regroupées les autres données.
Ces données prototypes sont appelés centroïdes ; en pratique l’algorithme associe chaque donnée à son centroïde le plus proche, afin de créer des clusters. D’autre part, les moyennes des descripteurs des données d’un cluster, définissent la position de leur centroïde dans l’espace des descripteurs : ceci est à l’origine du nom de cet algorithme (K-moyennes ou K-means en anglais).
Après avoir initialisé ses centroïdes en prenant des données au hasard dans le jeu de données, K-means alterne plusieurs fois ces deux étapes pour optimiser les centroïdes et leurs groupes :
1. Regrouper chaque objet autour du centroïde le plus proche.
2. Replacer chaque centroïde selon la moyenne des descripteurs de son groupe.
Après quelques itérations, l’algorithme trouve un découpage stable du jeu de données : on dit que l’algorithme a convergé.
Comme tout algorithme, K-means présente des avantages et des inconvénients : il est simple, rapide et facile à comprendre ; cependant il ne permet pas de trouver des groupes ayant des formes complexes.
L’exemple suivant s’appuie sur le célèbre jeu de données “Iris” qui décrit des fleurs par l’intermédiaire des longueurs et largeurs de leurs pétales et sépales. Les descripteurs considérés ici sont la longueur des sépales et la largeur des pétales. Chaque point correspond à une fleur et la couleur associée au point reflète son appartenance à un groupe. Les centroïdes de chaque groupe sont représentés par des croix, les frontières par des traits.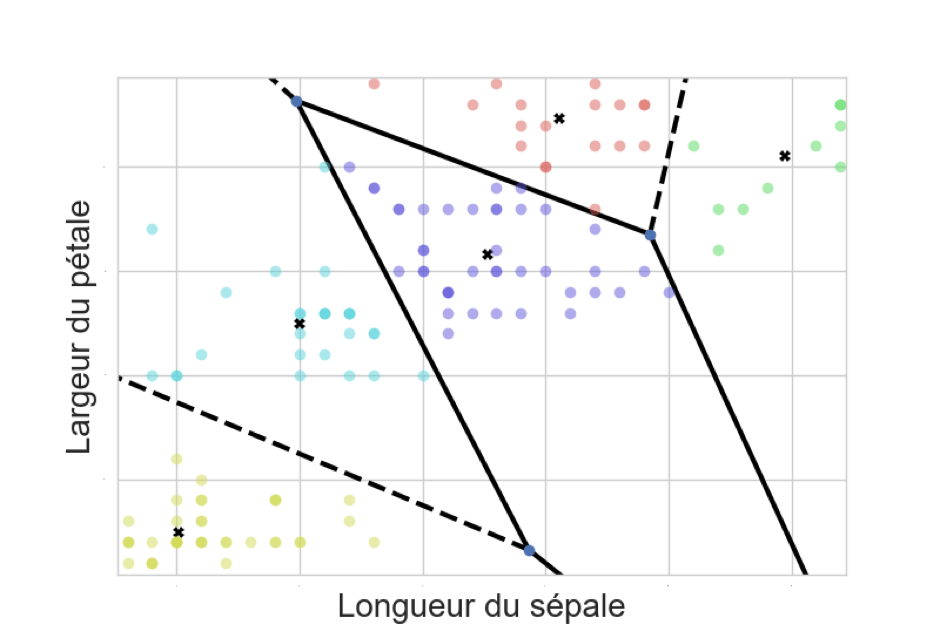
+ Retour à l'index