Quantités statistiques
Quantités statistiques : Les quantités statistiques sont des valeurs calculées à partir d’un jeu de données afin de caractériser certaines propriétés de sa distribution.
Les quantités statistiques sont des estimateurs de quantités réelles associées à la distribution. Elles dépendent du jeu de données et sont souvent qualifiées d’empiriques pour les distinguer des valeurs réelles.
Soit (Xi)1≤i≤n le jeu de données.
La plus connue des quantités statistiques est la moyenne m, qu’on appelle également « espérance empirique ». Elle est calculée par
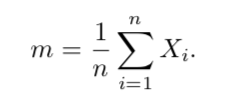
Elle représente la valeur moyenne des observations du jeu de données. Selon la loi des grands nombres, la moyenne converge vers l’espérance de la distribution quand le nombre de données tend vers l’infini.
L’écart-type empirique σ est donné par
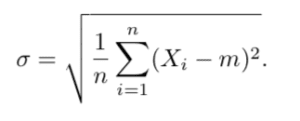
Il représente l’écart moyen des valeurs du jeu de données par rapport à sa moyenne m. Il sert à déterminer si les données sont dispersées dans l’espace ou resserrées autour de leur moyenne.
L’étude de l’écart-type est généralement complétée par l’analyse du Kurtosis empirique β, qui est une mesure indirecte de l’aplatissement de la distribution.
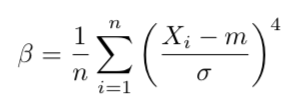
Pour finir, le coefficient d’asymétrie empirique γ (aussi appelé skewness) indique si la distribution a plutôt tendance à être plus grande que sa moyenne ou inversement.
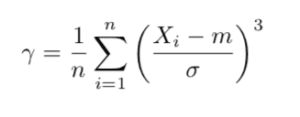
En plus de les décrire, ces quantités sont souvent utilisées pour distinguer des distributions : si deux jeux de données ont des quantités statistiques très différentes, alors ils n’ont probablement pas la même distribution (ce que l’on peut évaluer grâce à un « test statistique »).
Remarque : il existe une version non biaisée de chacun de ces estimateurs, c’est-à-dire dont l’espérance est égale à la valeur réelle estimée.
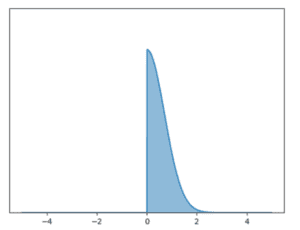
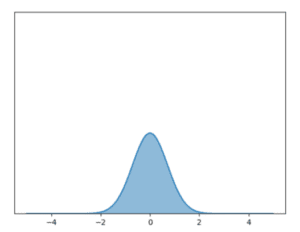
Exemples de distributions de caractéristiques différentes
- loi normale d’espérance 0 et d’écart-type 1
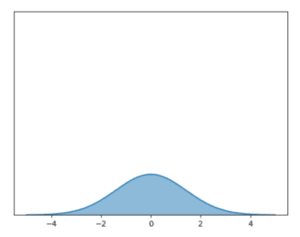
- loi normale d’espérance 0 et d’écarts-type 5
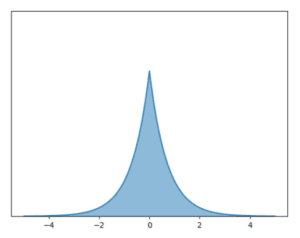
- loi d’espérance 0, d’écart-type 1 et de kurtosis positif
- loi d’espérance 0, d’écart-type 1 et de kutosis négatif
- loi d’écart-type 1 et de skewness positive
