Subspace clustering

Subspace clustering: Cette méthode d’apprentissage non supervisé est une extension de la méthode de clustering. Elle est utile pour regrouper des données définies par un grand nombre de descripteurs, autrement dit dans un espace à forte dimensionnalité.

Les algorithmes classiques de clustering visent à former des clusters, c’est à dire des groupes de données similaires. Afin de former ces groupes, ces algorithmes emploient différentes mesures de similarité entre les données dans l’espace des descripteurs, comme par exemple des mesures de distance entre les données. Cependant, la plupart des mesures existantes ont tendance à perdre leur discriminabilité, donc leur efficacité, lorsqu’elles sont utilisées dans des espaces à forte dimensionnalité.

Ce problème est une des conséquences, de ce que l’on appelle la “malédiction de la dimensionnalité”. Afin de le contrer et d’étendre le clustering aux espaces à forte dimensionnalité, plusieurs méthodes ont été proposées. Parmis elles figure le subspace clustering. Cette méthode vise, à la fois à retrouver les groupes de données similaires et à extraire les principaux descripteurs qui caractérisent chacun : chaque groupe de données est ainsi décrit uniquement par un ensemble pertinent de descripteurs, c’est à dire un sous-espace, ce qui permet de réduire la dimensionnalité de l’espace total.

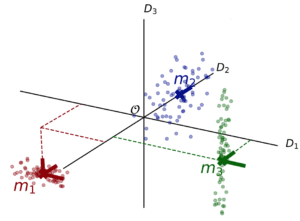
L’exemple suivant illustre le principe du subspace clustering avec des données décrites par trois descripteurs (D1, D2 et D3). Chaque point correspond à une donnée et chaque axe à un descripteur. Dans cet exemple, les données sont regroupées en trois clusters (m1, m2 et m3), symbolisés par leur couleur (rouge, bleu, vert). On constate que le groupe m1 est bien défini dans tout l’espace (descripteurs D1, D2 et D3), alors que le cluster m3 est décrit uniquement dans un sous-espace a deux dimensions (descripteurs D1 et D2), du fait que ses données sont uniformément réparties selon D3, ne décrivant aucun motif particulier selon cet axe.