SVM

SVM (Support Vector Machine ou Machine à vecteurs de support) : Les SVMs sont une famille d’algorithmes d‘apprentissage automatique qui permettent de résoudre des problèmes tant de classification que de régression ou de détection d’anomalie. Ils sont connus pour leurs solides garanties théoriques, leur grande flexibilité ainsi que leur simplicité d’utilisation même sans grande connaissance de data mining.

Les SVMs ont été développés dans les années 1990. Comme le montre la figure ci-dessous, leur principe est simple : il ont pour but de séparer les données en classes à l’aide d’une frontière aussi « simple » que possible, de telle façon que la distance entre les différents groupes de données et la frontière qui les sépare soit maximale. Cette distance est aussi appelée « marge » et les SVMs sont ainsi qualifiés de « séparateurs à vaste marge », les « vecteurs de support » étant les données les plus proches de la frontière.

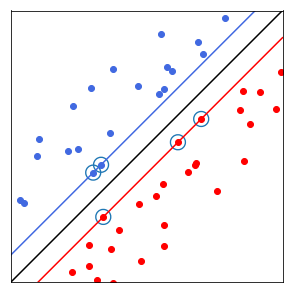
Légende (Crédit : © 2017, Julien Audiffren) : Dans cet espace à deux dimensions, la « frontière » est la droite noire, les « vecteurs de support » sont les points entourés (les plus proche de la frontière) et la « marge » est la distance entre la frontière et les droites bleue et rouge.

Cette notion de frontière  suppose que  les données soient linéairement séparables, ce qui est rarement le cas. Pour y pallier, les SVMs reposent souvent sur l’utilisation de « noyaux ». Ces fonctions mathématiques permettent de séparer les données en les projetant dans un feature space (un espace vectoriel de plus grande dimension, voir figure ci-dessous). La technique de maximisation de marge permet, quant à elle, de garantir une meilleure robustesse face au bruit – et donc un modèle plus généralisable.

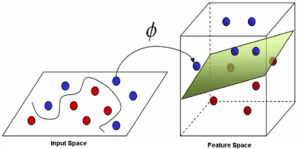
Légende (Crédit : © 2017, Haydar Ali Ismail, Medium.com Illustration of Support Vector Machine) : Les SVMs permettent de projeter les données dans une espace de plus grande dimension via une fonction noyau pour les séparer linéairement.

Les SVMs sont utilisés dans une variété d’applications (bioinformatique, recherche d’informations, vision par ordinateur, finance, etc.) notamment parce qu’à la différence des réseaux de neurones, on peut les utiliser sans comprendre leur fonctionnement : il existe des jeux d’hyperparamètres par défaut – pour la classification, la régression ou la détection d’anomalie – qui fonctionnent dans l’immense majorité des cas. C’est un de leurs principaux avantages. Ces hyperparamètres sont, par ailleurs, en nombre très réduit : ils se limitent au choix de la technique de régularisation (de type lasso ou encore régularisation RKHS*, une méthode spécifique aux SVMs) et au choix du noyau (noyaux polynomiaux, Sobolev, RBF**…). Concernant les algorithmes SVMs, citons le kernel ridge regression pour la régression ou le one class SVM pour la détection d’anomalie.

Enfin, selon les données, la performance des SVMs est en général de même ordre voire supérieure à celle d’un réseau de neurones ou d’un modèle de mélanges gaussiens, à l’exception de certains cas notables comme la classification d’images. Il a aussi été montré qu’en utilisant un noyau RBF, les SVMs deviennent un « approximateur universel » [1], c’est à dire qu’avec suffisamment de données, l’algorithme peut toujours trouver la meilleure frontière possible pour séparer deux classes (à condition que cette frontière existe).

[1] Wang, J., Chen, Q., & Chen, Y. (2004, August). RBF kernel based support vector machine with universal approximation and its application. In International Symposium on Neural Networks (pp. 512-517). Springer, Berlin, Heidelberg.

* RKHS :  Reproducing Kernel Hilbert Space ou espace de Hilbert à noyau autoreproduisant.

** RBF :  Radial Basis Function, désigne souvent le noyau gaussien.