
DeepMind dope le calcul matriciel avec AlphaTensor
⏱ 6 minDeepMind, la filiale IA de Google, était déjà connue pour avoir notamment développé AlphaGo (qui a battu des champions humains au jeu de go) et AlphaFold (qui prédit la conformation tridimensionnelle des protéines). Elle réalise cette fois un exploit dans le domaine des mathématiques avec son modèle AlphaTensor, qui découvre de nouvelles méthodes pour accélérer le calcul matriciel.
Une équipe de chercheurs de DeepMind a conçu et entraîné un nouveau modèle, AlphaTensor, qui est capable de découvrir de nouveaux algorithmes pour réaliser des produits matriciels le plus rapidement possible. Ces travaux ont été récemment publiés dans la célèbre revue scientifique Nature1. Le produit matriciel consiste à multiplier entre elles deux matrices, autrement dit des tableaux de nombres disposés en lignes et en colonnes, et produit une nouvelle matrice. Cette opération n’est possible que si le nombre de colonnes de la première matrice est égal au nombre de lignes de la seconde. Et le produit d’une matrice A de m lignes et n colonnes par une matrice B de n lignes et p colonnes est une matrice C de m lignes et p colonnes.
Pour calculer la valeur de chaque élément de la ligne i et de la colonne j de cette matrice produit (cij), on multiplie chaque élément de la ligne i de la première matrice (aik) par son homologue dans la colonne j de la seconde (bkj). Et c’est la somme de tous ces produits qui donne la valeur de cet élément cij. En d’autres termes, l’élément cij de C est obtenu en sommant les produits des éléments de la ième ligne de A par ceux de la jème colonne de B. Comme on peut le voir dans l’exemple ci-dessous.
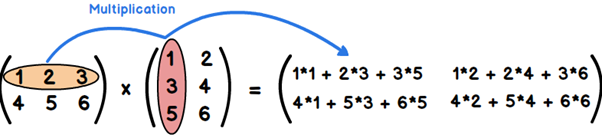
Le produit d’une matrice 2×3 par une matrice 3×2 est une matrice carrée 2×2.
Le calcul matriciel est impliqué dans de nombreux processus : traitement d’image, reconnaissance de la parole, simulation numérique, génération de graphiques sur ordinateur, compression de données, apprentissage automatique, etc. Il est donc important que ces calculs puissent être effectués le plus rapidement possible. Or, le produit matriciel est une opération coûteuse. Pour calculer le produit d’une matrice de m lignes de n colonnes par une autre de n lignes et p colonnes, il faut effectuer m×n×p multiplications et m×p additions. Dans le cas de deux matrices de dix par dix, par exemple, cela représente mille multiplications, et cent additions. Or, sur un ordinateur, le temps d’exécution d’une multiplication est plus long que celui d’une addition, les multiplications “coûtent” généralement bien plus cher que les additions. C’est pourquoi des mathématiciens cherchent depuis longtemps des algorithmes de multiplication de matrices plus économes en multiplications.
Un premier pas : l’algorithme de Volker Strassen
En 1967, le mathématicien allemand Volker Strassen obtient enfin un premier résultat dans ce domaine. Il met au point un algorithme qui permet de multiplier deux matrices carrées, possédant le même nombre de colonnes et de lignes, peu importe leur taille, avec moins de multiplications que l’algorithme trivial. Prenons le cas précis des matrices 2×2 (deux lignes, deux colonnes). Il s’agit de calculer la matrice C, produit de A par B :
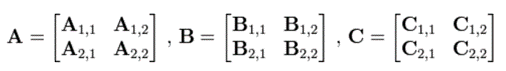
En utilisant la méthode conventionnelle, il faut effectuer 8 multiplications :
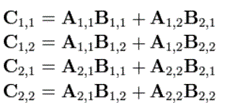
L’algorithme de Strassen commence par calculer sept valeurs intermédiaires :
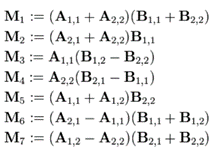
Puis il calcule chaque élément de la matrice résultat C à partir de ces résultats intermédiaires :
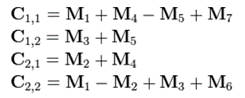
Pour deux matrices carrées de taille 2, l’algorithme de Strassen permet ainsi de passer de huit multiplications à sept, soit une de moins que la méthode conventionnelle. Notons que ce résultat est obtenu au prix de quatorze additions supplémentaires. Autre exemple, pour multiplier deux matrices carrées de taille quatre, la technique conventionnelle oblige à faire 64 multiplications différentes, tandis que l’algorithme de Strassen fait passer ce nombre à 49, soit 15 en moins. Un gain de temps non négligeable pour un logiciel qui répéterait souvent ce type de calcul.
L’équipe de DeepMind a construit et entraîné un modèle par apprentissage profond qui a découvert de nouveaux algorithmes de multiplication de matrices, plus rapides que l’algorithme trivial et même meilleurs que celui de Volker Strassen. Pour cela, elle a converti la recherche de ces algorithmes en un jeu. Un jeu… à un seul joueur. Et pour construire son modèle, elle a pris comme point de départ AlphaZero, un réseau de neurones capables d’apprendre à jouer (et gagner) à divers jeux, notamment au jeu de go et aux échecs. Il généralise AlphaGo, qui est devenu célèbre pour avoir battu des champions au jeu de go. Cette fois, il s’agit de jouer à chercher de nouveaux algorithmes de multiplication de matrices… Un jeu particulièrement ardu, puis que le nombre de combinaisons de “coups” possibles est largement supérieur à celui auquel fait face un joueur de go.
Apprentissage hybride, supervisé et par renforcement
Pour entraîner son modèle, l’équipe avait besoin d’un bon jeu de données, qu’il n’était pas aisé de construire et d’annoter “à la main”. Elle a donc développé un outil capable de générer en quantité des “données synthétiques” pour constituer un copieux dataset. AlphaTensor a ensuite été entraîné à partir de ce jeu de données, donc en mode supervisé, mais également en faisant appel à l’apprentissage par renforcement. C’est ce que nous précise Alhussein Fawazi, le premier signataire de la publication dans Nature : « Dans AlphaTensor, nous utilisons des exemples supervisés synthétiques, que nous avons conçus nous-même. Cependant, se fier entièrement à ces données n’est pas suffisant. C’est pour cela que nous avons fait le choix d’avoir une approche hybride qui reprend certains fondements de l’apprentissage supervisé et de l’apprentissage par renforcement. Elle s’est avérée être la stratégie la plus efficace pour mettre au point notre modèle ».
Grâce à AlphaTensor, les chercheurs ont réussi à découvrir des algorithmes efficaces, et même plus performants que l’algorithme de Strassen. En guise d’exemple, pour deux matrices 4×4, AlphaTensor réussit à les multiplier en utilisant 47 multiplications contre 49 avec l’algorithme de Strassen et 64 pour la technique usuelle. Pour des matrices plus grandes, le résultat est aussi sans équivoque et permet de gagner du temps et de faire moins de multiplications. « La découverte réalisée par DeepMind est exceptionnelle, estime François Le Gall, chercheur en mathématiques à l’Université de Nagoya (Japon) et spécialiste du calcul matriciel. C’est sans doute la première fois que l’intelligence artificielle arrive à prouver un résultat qui a résisté à tous les mathématiciens jusqu’à présent ».
Des résultats encourageants
Pour mieux expliciter le gain en efficacité obtenu grâce à AlphaTensor, François Le Gall fait appel à une mesure de la complexité des algorithmes, qui comptabilise le nombre d’étapes de calcul nécessaires pour obtenir un résultat et l’exprime en “temps” : c’est ce que l’on appelle la “complexité en temps”. « L’algorithme mis en avant par AlphaTensor calcule le produit de deux matrices n x n en O(n2.78) opérations, contre O(n2.81) opérations pour l’algorithme de Strassen, et O(n3) opérations pour la méthode conventionnelle », nous précise François Le Gall.
Du côté de DeepMind, les chercheurs veulent aller plus loin et s’appuyer sur ces résultats pour chercher à résoudre d’autres problèmes mathématiques non résolus. « Nous allons nous appuyer sur toutes nos précédentes recherches et exploiter, sans doute, le deep learning, pour mettre en place à l’avenir des modèles d’IA qui pourront faire avancer les mathématiques » affirme Alhussein Fawzi. François Le Gall est également persuadé que l’IA pourra faire des merveilles à l’avenir, notamment en mathématiques : « Il est très probable que l’intelligence artificielle devienne un outil indispensable […], ce qui est d’un certain côté révolutionnaire ».
Toutefois, quelques jours seulement après la découverte réalisée par les chercheurs de DeepMind, Manuel Kauers, un célèbre mathématicien autrichien, accompagné d’un doctorant, Jakob Moosbauer, ont également mis au point un algorithme pour le calcul matriciel, encore plus rapide que celui proposé par AlphaTensor pour un cas particulier : la multiplication de matrices 5×5. Ils ont publié leurs travaux2 sur arXiv, et contrairement aux chercheurs de DeepMind, les deux mathématiciens n’ont pas fait appel à l’intelligence artificielle pour mettre au point leur algorithme. Comme quoi, l’intelligence humaine a encore de beaux jours. Mais l’intelligence artificielle n’a pas dit son dernier mot…
Zacharie Tazrout
1. Alhussein Fawzi et al. Discovering faster matrix multiplication algorithms with reinforcement learning. Nature, 2022. doi.org
2. Manuel Kauers, Jakob Moosbauer. The FBHHRBNRSSSHK-Algorithm for Multiplication in Z25×5 is still not the end of the story. arXiv, 2022. doi.org








