
Optimiser la prévision de consommation électrique à l’échelle locale
⏱ 7 minVirginie Dordonnat, data scientist chez RTE (Réseau de transport d’électricité)
En France, pour éviter les pannes, la surcharge du réseau électrique ou les coupures de courant, RTE (Réseau de transport d’électricité) est le garant de l’équilibre permanent entre la consommation d’électricité et sa production. Dans le cadre d’une thèse, l’entreprise développe de nouveaux modèles de prévision de la consommation, en cherchant à identifier puis à exploiter des comportements de consommation similaires selon un maillage local. Un défi qui devrait améliorer la qualité des prévisions nationales.
Comment est assuré l’équilibre national entre consommation et production électrique ? D’une part, en prévoyant la consommation, ce qui permet d’anticiper les moyens de production d’électricité à mettre en œuvre. D’autre part, en évaluant la production d’énergies renouvelables, comme l’énergie éolienne ou solaire, prioritaires sur le réseau électrique car « fatales », au sens où elles seraient perdues si on ne les utilisait pas au moment où elles sont disponibles. Autrement dit, toute l’électricité renouvelable produite est acheminée sur le réseau et c’est la production d’énergie d’origine nucléaire ou thermique qui s’adapte, par exemple en diminuant ou en augmentant la production d’une centrale thermique. Concrètement, cet équilibre consommation/production nécessite notamment de coupler des modèles mathématiques de prévision de la consommation électrique avec des modèles de prévision de la production d’énergie renouvelable.
De l’échelle nationale à l’échelle locale
De quoi dépend la consommation électrique en France ? Au niveau national, elle est d’abord fonction des caractéristiques saisonnières, avec une forte thermosensibilité en hiver, et dans une moindre mesure en été. Elle est également liée aux cycles d’activités horo-hebdomadaires, avec notamment une moindre demande la nuit et les week-ends. Cette consommation nationale « lisse » en quelque sorte les variations locales de consommation. Néanmoins, pour que l’électricité puisse être acheminée partout où elle est demandée, il faut également s’intéresser à l’échelle locale, tenir compte de la configuration du réseau électrique et de la situation géographique des moyens de production. Ainsi, par exemple, si une ligne électrique connaît un défaut, il faut que le reste du réseau environnant puisse assurer le transit pour prendre le relais. Il est alors nécessaire de bien prévoir la consommation aux environs de la ligne en défaut. Celle-ci est évaluée notamment au niveau des postes électriques (transformateurs), frontières entre le réseau de transport Les réseaux de transport acheminent l’électricité des centres de production (comme les centrales) vers les zones de consommation, grandes agglomérations ou grandes entreprises. S’échelonnant entre 50 000 volts à 400 000 volts, leurs lignes électriques sont à haute tension (HT) et à très haute tension (THT). (à haute et très haute tension) et les réseaux de distribution Les réseaux de distribution reçoivent l’électricité des réseaux de transport et la distribuent aux consommateurs. S’échelonnant entre 110 volts et 50 000 volts, leurs lignes sont à basse tension (BT) et à moyenne tension (MT). Une part de plus en plus importante de la production éolienne et solaire est directement raccordée aux réseaux de distribution. (à moyenne et basse tension), ceux qui acheminent l’électricité jusqu’aux consommateurs, qu’il s’agisse de particuliers ou d’entreprises.
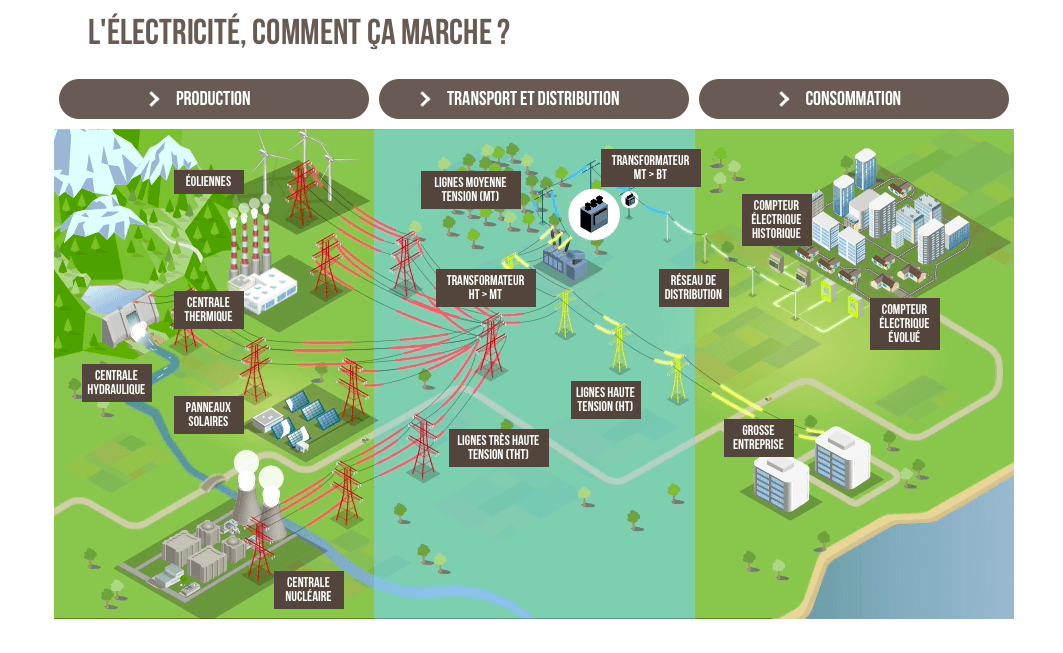
Ce petit module, réalisé par la Commission de régulation de l’énergie montre comment s’articulent production, transport, distribution et consommation d’électricité.
Une des missions de RTE consiste à développer des modèles de prévision de la consommation électrique à cette maille locale, au niveau des postes électriques qui relient le réseau de transport à celui de distribution. Cela à plusieurs horizons : du court-terme (de l’infra-journalier à J+2) au long-terme (pour alimenter des études concernant des investissements futurs sur le réseau électrique). Or, il est particulièrement difficile d’avoir des historiques stables à cette échelle. Cela représente donc un défi en termes de prévisions quotidiennes, car les caractéristiques de consommation sont très variables localement selon les usages de l’électricité, autrement dit selon les comportements des consommateurs reliés, notamment professionnels : par exemple, deux postes électriques peuvent avoir leurs pointes de consommation à des moments différents de la journée. À cette échelle locale, les consommations saisonnières sont également moins stables d’une année sur l’autre du fait de l’évolution des activités économiques locales.
Exploiter les similarités locales
En opérationnel, RTE utilise une approche top-down, c’est-à-dire la désagrégation de prévisions régionales, pour obtenir des prévisions aux postes. Par ailleurs, les modèles additifs généralisés (GAM) ont été proposés pour estimer indépendamment la consommation de chaque poste[1]. La première approche conserve par construction la cohérence entre les prévisions locales et les prévisions régionales. La seconde n’utilise que l’information propre à chaque poste, ce qui permet un calcul rapide, mais n’exploite pas les similarités de consommation qui peuvent exister entre les postes.
Pour améliorer nos prévisions, nous développons un modèle fondé sur une approche de modélisation locale enrichie par des informations simultanées sur tout ou partie des postes électriques. Cela augmente fortement la complexité du problème, il faut donc poser des contraintes : nous avons choisi d’exploiter les similarités de consommation entre les différents postes électriques, qu’elles soient d’ordre géographique et/ou d’usage de l’électricité. Par exemple, deux postes à proximité ont de fortes chances d’avoir une météo locale comparable et des modes de chauffage similaires. De même que deux postes électriques proches de stations de ski auront, a priori, des comportements comparables. Cela nous permettrait de parvenir à une modélisation, simultanée cette fois, des quelques 2 500 postes de consommation électriques (hors grands clients industriels) que compte le réseau national.
L’objectif est que le modèle soit capable d’analyser les données de consommation pour détecter ces similarités de façon automatique. L’estimation du modèle doit également être raisonnable en temps de calcul et en capacité de mémoire, malgré une volumétrie de données importante, les prévisions étant ensuite instantanées. RTE finance la thèse de Benjamin Dubois pour sonder les différentes méthodes d’optimisation de ce type de modèle de prévision. Encadré par Guillaume Obozinski et Jean-François Delmas, de l’École des Ponts ParisTech (ENPC), le travail de Benjamin Dubois consiste à explorer les méthodes combinant des matrices de rang faible et des matrices parcimonieuses.
Des modèles à court et à moyen termes
Pour une bonne prévision de consommation à la maille locale, nous développons deux types de modèles, respectivement à court et à moyen termes. Les modèles dits de court terme sont fondés sur les dernières réalisations de consommations (fiabilisées au cours du temps), sur des prévisions météorologiques (température et couverture nuageuse/ensoleillement) ainsi que sur des données calendaires (heure, jour de la semaine, jour de l’année, jours fériés ainsi que leur veille et lendemain, vacances scolaires, changement d’heure). Les modèles de moyen terme, quant à eux, ne disposent pas des dernières informations de consommation.
Le contexte naturel de modélisation pour exploiter les similarités est celui de la « régression multitâche » aussi appelée régression multivariée ou prévision conjointe : chaque observation y(t), où t est le temps, est un vecteur dont chaque élément correspond à un poste électrique. Comme expliqué ci-dessus, on cherche à exploiter les similarités géographiques et/ou économiques entre éléments du vecteur. En soi, la modélisation indépendante de la consommation par poste ne pose pas de difficulté algorithmique particulière. L’estimation conjointe de la consommation de plusieurs postes nécessite, quant à elle, de poser des contraintes liant les postes entre eux, ce qui a pour conséquence d’augmenter la dimension du problème.
Formulation mathématique
Du point de vue de la formulation, le modèle de régression multitâche s’écrit classiquement : ![]() , Y étant ici une matrice de consommations horaires (et non un vecteur), X la matrice des variables explicatives et B la matrice des coefficients de régression. Les variables explicatives ne sont pas les données météorologiques ou calendaires initiales, mais des transformations (sur des bases splines par exemple), afin de tenir compte de la non-linéarité du lien à la consommation électrique. Certaines variables correspondent à des interactions entre variables explicatives initiales.
, Y étant ici une matrice de consommations horaires (et non un vecteur), X la matrice des variables explicatives et B la matrice des coefficients de régression. Les variables explicatives ne sont pas les données météorologiques ou calendaires initiales, mais des transformations (sur des bases splines par exemple), afin de tenir compte de la non-linéarité du lien à la consommation électrique. Certaines variables correspondent à des interactions entre variables explicatives initiales.
Sans contraintes supplémentaires, le modèle de régression multitâche est équivalent à un ensemble de modèles de régressions séparés et revient à modéliser les postes séparément. Notons, par ailleurs, que l’exploitation des interactions entre variables explicatives a été relativement peu étudiée pour cette problématique. Pour prendre en compte les similarités entre postes dans ce problème multitâche, nous avons choisi de poser une contrainte de rang faible sur la matrice B : ainsi, les différents postes vont partager l’information des variables explicatives contenues dans la matrice X via un nombre réduit de combinaison linéaires de ces variables.
Autre difficulté, si l’on tient compte de toutes les interactions possibles, le nombre de régresseurs du problème peut être du même ordre que le nombre d’observations. Nous introduisons donc également une pénalité de type L1 par bloc, pour induire la mise à zéro de lignes entières de la matrice B et privilégier ainsi l’approche parcimonieuse comme en régression LASSO.
Le problème considéré s’écrit : ![]() , avec la contrainte sur le rang de la matrice B, rg(B)
, avec la contrainte sur le rang de la matrice B, rg(B)![]() et où
et où ![]() est la somme des normes L2 des lignes de la matrice B. L’hyper-paramètre λ est à optimiser : plus sa valeur est élevée, plus il y aura de lignes de coefficients nuls dans B. Le rang r est aussi un hyper paramètre à optimiser : plus r est faible, plus le partage d’information est important.
est la somme des normes L2 des lignes de la matrice B. L’hyper-paramètre λ est à optimiser : plus sa valeur est élevée, plus il y aura de lignes de coefficients nuls dans B. Le rang r est aussi un hyper paramètre à optimiser : plus r est faible, plus le partage d’information est important.
Vers un modèle opérationnel
Les travaux menés pendant la thèse se concentrent principalement sur la formulation adéquate du modèle et sur la façon de prouver des conditions de convergence d’une méthode d’optimisation adaptée pour une estimation suffisamment rapide en pratique. Dans cette optique, la recherche du modèle « idéal » de consommation locale n’est pas primordiale. Dans un second temps, et avec une analyse plus poussée des données, l’objectif sera d’améliorer les modèles pour atteindre, cette fois, des performances satisfaisantes en termes de prévision de consommation à la maille locale. Pour cela, il faut trouver une valeur de r adaptée. La solution optimale pourra consister à considérer plusieurs groupes de postes (et donc plusieurs modèles de rangs faibles) plutôt que l’ensemble des postes à la fois. Les modèles testés sont de types additifs, et prennent en compte les interactions entre les différentes variables du problème. La difficulté pratique est d’obtenir un modèle contenant la « bonne » sélection de variables parmi le grand nombre disponible en entrée de l’optimisation.
Comme pour tout modèle, son passage à la phase opérationnelle nécessitera des adaptations. Pour l’instant, dans le cadre de la thèse, le jeu de données a été simplifié de manière à ne prendre en compte que les facteurs de consommation, et non les changements de topologie du réseau (des modifications liées à des travaux sur le terrain par exemple). Ces changements induisent de grands écarts de consommation et des ruptures dans le signal qui seront, à terme, à anticiper.
[1]Y. Goude, R. Nedellec & N. Kong, « Local Short and Middle Term Electricity Load Forecasting With Semi-Parametric Additive Models », IEEE Transactions on Smart Grids, vol.5 n° 1, January 2014
Pour en savoir plus :
Benjamin Dubois, Jean-François Delmas, Guillaume Obozinski. Fast Algorithms for Sparse Reduced-Rank Regression. International Conference on Artificial Intelligence and Statistics, 2019. Publication en cours.
llustration à la une : © Commission de régulation de l’énergie








